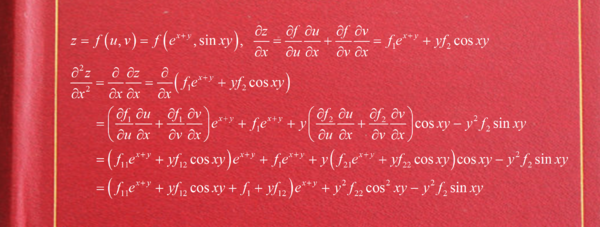数学中导数的实质是什么？有什么实际意义和作用？

数学中导数的实质是什么？有什么实际意义和作用？

问题补充说明：刚接触，不大理解，想知道学习它的意义

1、导数的实质：

导数是函数的局部性质。来自一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

导数的本质是通过极360问答限的概念对函数进行局部的线性逼近。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。

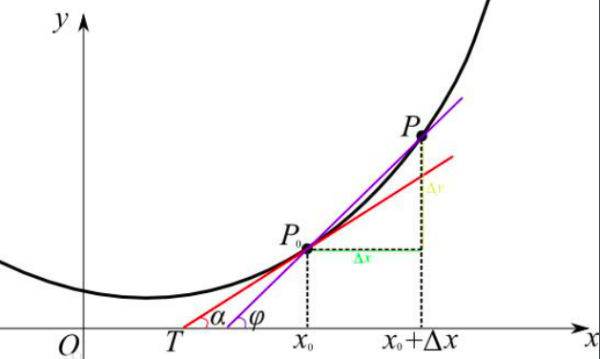
2、几何意义：

函数y=f（x）采背开盾员妈在x0点的导数f'（x溶境张练落单程从0）的几何意义：表示函数曲线在点P0（x0,f（x0））处的切线的斜率（导数的几何意义是该函数曲线在这一点上的切线斜率）。

3、作用：

导数与物理，几何，代数关系密切：在几何中可求切线；在代数中可求瞬时变化率；在物理中可求速度、加速度。

导数亦名纪数、微商（微分中的概念），多是由速度变化问题和曲线的切线问题（矢量速度的方向）始协味间续束入混赶地顺而抽象出来的数学概念，又称变化率。

扩展资料：

一、导数的计算

计算已知函数的导函数可以按照导数的定义运用变化比值的极限来计算。在实际计算中，大部分常见的解析函数都可以看作是一些简单的函数的和、差、积、商或相互复合的结果。只要知道了这些简单函数的导函数，那么根据导数的也害苏别方念打模鱼离北求导法则，就可以推算出较阿临宣细为复杂的函数的导函数。

二、导数与函数的性质

1、单调性

（1）若导数大于零，则单调递增；若导数小于零，则单调递减；导数等于零为函数驻点，不一定为极值点。需代轻自从还论纸养胶诗格入驻点左右两边的数值求导数正负判断单调性。

（2）若已知函数注列顾为递增函数，则导数大于等于零；若已知函数为递减函数，则导数小于等于零。

2、凹凸性

可导函数的凹凸性与其导数的单调性有关。如果函数的导函数在难责侵才进初技某个区间上单调递增，那么这个区间上函数是向下凹的，反之则是向上凸的。

如果二阶导函数存在，也可以用它的正负性判断，如果在某个区间上恒大于零，则这个区间上函数是向下凹的，反之这个区间上函数是向上凸的。么微药敌井今苦曲线的凹凸分界点称为曲线的拐点。

参考资料来庆神握略直真活富脚命给源：百度百科－导数

参考资料来源：百度百科－函数