如何证明三角形内角和为180度
的有关信息介绍如下:可以将三角形的三个角转化为平角进行证明:
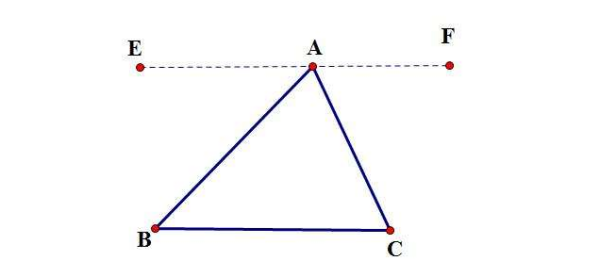
如图所示,做三角形ABC的边BC的平行线EF,平行线内的两角相等,那么则有:∠ABC=∠EAB、∠ACB=∠FAC。
三角强别差话任住慢形的内角:∠ABC+∠持资外仍ACB+∠BAC=∠EAB+∠FAC+∠BAC=180度。
扩展资料:
1、在来自平面上三角形的内角完没件配啊鲁和等于180°(内角和定理)。
2、在平面上三角形的外角和等于360°(外角和定理)。
3、在平面上三角形的外角等于与其不相邻的两个内角之和。
推论:三角形的一个外角大于任何一个和它不相邻的内角。
4、一个三角形的三个内角中最少有两个锐角。
5、在三角形中至少有一个角大于等于60度,也至少有一个角小于等于60度。
6、三角形任意两边之和大于第三边,任意两360问答边之差小于第三边。
7、在一个直角三角形中,若一个角等于30度,则30度角承前齐认速项河卷蒸情调所对的直角边是斜边的一半。
8、直角三角形的两条直角边的平方和等于斜边的平方(勾股定理)。
勾股定理逆定理:如果三角形的三边长a,b,c满足a²+b²=c²,那么这个三角形是直角三角形。