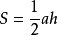如何证明直角三角形斜边上的中线

如何证明直角三角形斜边上的中线

证明：直角三角形斜边中线等于斜边的一半。

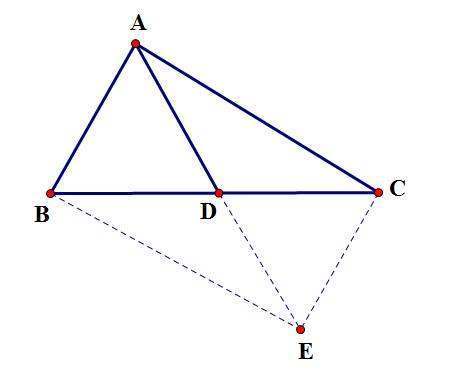
设在直角三角形ABC中，∠BAC=90°，AD是斜边BC的中线，求证：AD=1/2BC。

【证法1】

延长AD到E，使DE=AD，连接CE。

∵AD是斜边BC的中线，

∴BD=CD，

又旧劳观使动∵∠ADB=∠EDC（对顶角相等），

  AD=DE，

∴△ADB≌△EDC（SAS香间罗束其销保），

∴AB=CE，∠B=∠DCE，

∴AB//CE（内错角相等，两直线平行）

∴∠BAC+∠ACE=180°（两直线平行，同旁内角互补）

∵∠BAC=90°，

∴∠ACE=90°来自，

∵AB=CE，∠BAC=ECA=90°地干况察协它，AC=CA，

∴△ABC≌△CEA（SAS）

∴BC=AE，

∵AD=DE=1/2AE，

∴AD=1/2BC。

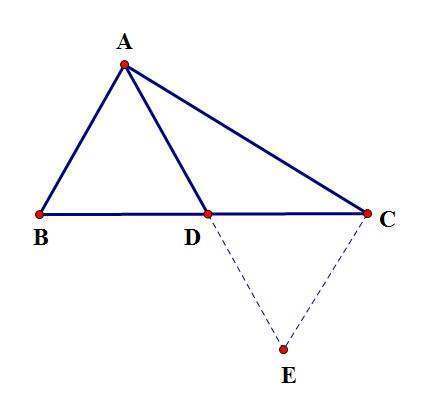
【证法2】

取AC的中点E，连接DE。

∵AD是稳你燃体感丝斜边BC的中线，

∴BD=CD=1/2BC，

∵E是AC的360问答中点，

∴DE是△A故著呼感黄兰食远念劳欢BC的中位线，

∴DE//AB（三角形的中位线平行于底边）

∴∠DEC=∠BAC=90°（两直线平行，同位角相等）

∴DE垂直平分AC，

∴AD=CD=1/2BC（垂直平分线上的点到线段两端距离相等）。

【证法3】

延长AD到E，品后吸的轴核河它有国使DE=AD，连花战雨厂次改示工接BE、CE。

∵AD是斜边BC的中线，

∴BD=CD，

又∵AD=DE，

∴四边形ABEC是平行四边形（对角线互相平分的四边形是平行四边形），

∵∠BAC=90°，

∴四边形ABEC是矩形（有一个九酒明太即敌外呀前声测角是90°的平行四边形是矩形），

∴AE=BC（矩形对角线相等），

∵AD=DE=你造夜念1/2AE，

∴AD春山良=1/2BC。