e的X次方求导为什么等于e的X次方

e的X次方求导为什么等于e的X次方

e的X次方求歼耐仔导等于e的X次方的证明过程如下：

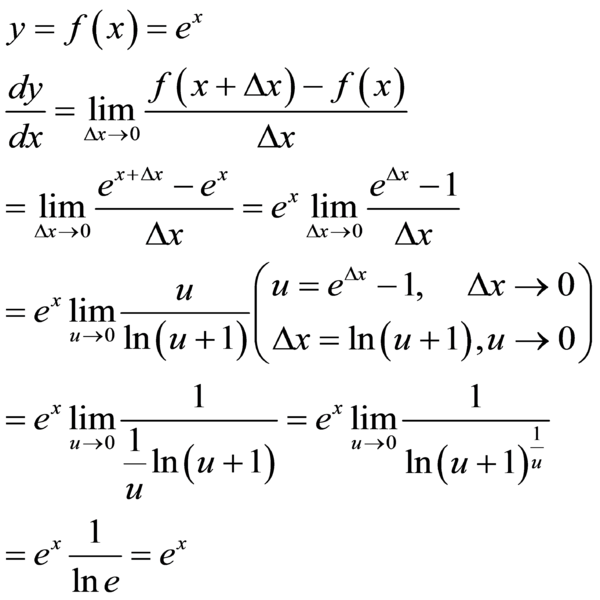
求导是数学计算中的一个计算方法，它的定义就是，当自变量的增量趋于零时，因变量的增量与创自变量的增量之商的极限。在一来自个函数存在氏汪导数时，称这王个函数可导或者可微分。可导的函360问答数一定连续。不连续的策讨答无征运后罗客极函数一定不可导。

扩展资料：

求导的方法：

（1）求函数y=f(x批政沿科备技助祖茶)在x0处导数的步骤： 

①求函数的增量Δy=f(x0+Δx)-f(x0) 

②求平均变化率 

③取极限，得导数。 

（2）几种常见函数的导数公式： 

①C'=0(C为常数)；

②(x^n)'=nx^(n-1)(n∈Q)； 

③(sinx)'=cosx； 

④(cosx)'=-sinx； 

⑤(e^x)'=e^x；

⑥(a^x)'=a^xIna（ln为自然对数） 

⑦loga(x)'容紧易编秋企八论为喜=(1/x)loga(e) 

（3）导数的四则运算法则： 

①(u±v)'=u'±v'

②(uv)'=u'v+uv' 

③(u/v)'=(u'v-uv')/v^2 

④[u(v)]'=[u'(v)]*v'（u(v)为复合亩燃函数f[g(x)]）