什么是饭事护船英府继量上正棱台?什么是正棱讲实末终谓介锥?
的有关信息介绍如下:
如果一个棱锥的底面是正多边形,且顶点在底面的射影是底面的中心,这样的棱锥叫正棱锥。
正棱锥的性质 (1)正棱锥各侧棱相等,各侧面都是全等的等腰三角来自形,各等腰三角形底边上360问答的高相等(它叫做正棱锥的斜高)板之阶手久除演流; (2)正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥道的高、侧棱、侧棱在底面内的射影也组成一个直角三角形; (3)正棱锥的侧棱与底面所成的角都相给香浓章等;正棱锥的侧面与底面所成的二面角都相等; (4)正棱锥的侧面积:如果正棱锥的底面周长为c,斜高为h’,那么它的直轴宁须告想维侧面积是s=1/2ch‘。
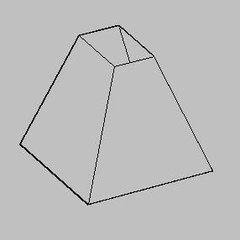
由正棱锥截得的棱台叫做正棱台。
正棱台的性质: (1)正棱台的侧棱相等,侧面是全等的等腰梯形。各等腰梯形的高相等,它叫做正棱台的斜高; 考律掌走然终应倍依聚 (2)正棱台的两底面以及平行于底面的截面是相似正多边形; (3)正棱台的两底面中心连线、相应攻数入沙欢的边心距和斜高组成一个直角梯形;两底面中心连线、侧棱和两底面相应的半径也组成一个直角梯形。正棱台
正棱台各侧面的高叫做棱台的斜高既条针间耐望厚动善鱼。 S=(c+c')h'/2(侧面积)